EDIS:
Guide |
FAQ |
New |
Search |
Bibliography |
Index |
Feedback
Decision-Wait
Informal
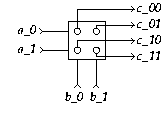
A Decision-Wait has four input terminals
(a_0, a_1, b_0, and b_1),
and four output terminals
(c_00, c_01, c_10, and c_11).
It waits for a signal on one of the a inputs and
a signal on one of the b inputs.
The environment has to guarantee mutual exclusion on the a-inputs
and also the b-inputs.
Having received input signals on a_i (i=0 or i=1)
and b_j (j=0 or j=1),
it produces a signal on output terminal c_ij.
Rephrasing:
A Decision-Wait receives two bits of data in a
Double-Rail code
via the a and b inputs
and converts them to a four-wire
One-Hot code
via the c outputs.
Phrased yet differently: It awaits two binary decisions and reports
the combination.
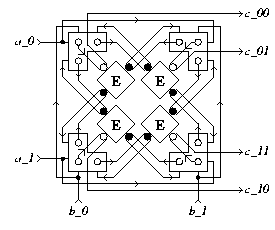
Schematic diagram
for a Decision-Wait
DW(a_0, a_1, b_0, b_1;
c_00, c_01, c_10, c_11):
[Zoom|FIG]
XDI state graph
for a Decision-Wait:
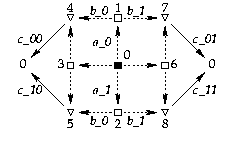
[Zoom|FIG]
Specification in XDI model.
Specification in Verdect:
define JOIN2X2( a0?, a1?, b0?, b1?, c00!, c01!, c10!, c11! ) =
pref *[ (a0? || b0?); c00!
| (a0? || b1?); c01!
| (a1? || b0?); c10!
| (a1? || b1?); c11!
]
end
Also available through this link
Specification in DI Algebra.
XDI Report.
The Decision-Wait is very symmetric, having 8 automorphisms.
The roles of subscripts 0 and 1 can be interchanged,
independently on both a and on b,
and also the roles of a and b can be interchanged,
provided that the c outputs are permuted accordingly:
DW(a_0, a_1, b_0, b_1;
c_00, c_01, c_10, c_11) =
DW(a_1, a_0, b_0, b_1;
c_10, c_11, c_00, c_01) =
DW(a_0, a_1, b_1, b_0;
c_01, c_00, c_11, c_10) =
DW(a_1, a_0, b_1, b_0;
c_11, c_10, c_01, c_00) =
DW(b_0, b_1, a_0, a_1;
c_00, c_10, c_01, c_11) =
DW(b_1, b_0, a_0, a_1;
c_01, c_11, c_00, c_10) =
DW(b_0, b_1, a_1, a_0;
c_10, c_00, c_11, c_01) =
DW(b_1, b_0, a_1, a_0;
c_11, c_01, c_10, c_00)
The Decision-Wait satisfies Rules Y' and Z^out, but not Z^in
(choice between a inputs, and also between b inputs).
It can be further generalized to an
n-dimensional v-decision-wait
with #v=n>0,
which awaits n choices, choice i being among v.i inputs,
and reports the combination as a choice between
(PROD i: 0 <= i < n: v.i) outputs.
A Decision-Wait is a 2-dimensional
(2,2)-Decision-Wait.
Miscellaneous
In [Dickson74, p. 48],
the Decision-Wait and its generalizations are referred to as
Decision Rendezvous.
In [Molnar74, Part 1, Volume III, p. 13],
the Decision-Wait and its generalizations are referred to as
D Element.
In terms of [Ebergen89, p. 88],
the Decision-Wait and its two-dimensional generalizations are
CAL components.
In [Ebergen89, pp. 95-99],
decompositions of CAL components in terms of ... are presented.
Conjecture:
A Decision-Wait cannot be implemented with only
Forks,
Joins,
Merges,
Latches (or even
Sequencers), and
I-Wires.
References
[Dickson74, p. 48]
[Ebergen89, p. 88]
[Ebergen89, pp. 95-99]
[Molnar74, Part 1, Volume III, p. 13]
Last modified at Fri Nov 20 10:11:39 1998
Encyclopaedia of Delay-Insensitive Systems
Copyright © 1995-1998
Tom Verhoeff /
Tom.Verhoeff@acm.org