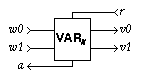
The environment of a Non-Receptive 1-Bit Variable must guarantee mutual exlusion of the signals on w0 and w1. In contrast to a 1-Bit Variable, the environment must also guarantee mutual exclusion between the write and read inputs.
Note that a Non-Receptive 1-Bit Variable stores a proper initial value. That is, before the first write operation, all read operations will return the same value. This initial value, however, is not prescribed.
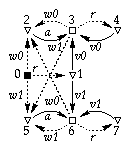
Specification in Verdect:
define VAR( w0?, w1?, a!, r?, v0!, v1! ) =
|[ x0, x1, y0, y1 ::
pref *[ (w0?; x0 | w1?; x1); a!
| r?; (y0; v0! | y1; v1!)
]
|| pref (( *[y0] | *[y1] ); *[ x0; *[y0] | x1; *[y1] ])
]|
end
Also available through this link
This
verification report
compares the Verdect specification with the XDI specification.
Specification in DI Algebra:
NAME = (Non receptive one bit variable)
I = { w0, w1, r }
O = { v0, v1, a }
V = V0 ND V1
V0 = [w0? -> V0W, w1? -> V1W , r? -> V0R]
V1 = [w0? -> V0W, w1? -> V1W , r? -> V1R]
V0W = [a! -> V0, r? -> CHAOS, w1? -> CHAOS]
V1W = [a! -> V1, r? -> CHAOS, w0? -> CHAOS]
V0R = [v0! -> V0, w0? -> CHAOS, w1? -> CHAOS]
V1R = [v1! -> V1, w0? -> CHAOS, w1? -> CHAOS]
.
Also available through this link
This
verification report
compares the DI Algebra specification with the XDI specification.
The subscripts 0 and 1 can be interchanged systematically.
A Non-Receptive 1-Bit Variable is not output deterministic, since there is an output choice in state 1. The output nondeterminism is static.
No information available
No information available
No information available
No information available