Sequencer

Specifications

Informal

A Sequencer has three input terminals (a_0, a_1, and b), and two output terminals (c_0 and c_1). It waits for a signal on at least one of the a_i inputs and a signal on the b input. In contrast to a Latch, the environment need not guarantee mutual exclusion of the a_i-inputs. Having received input signals on a_i (i=0 or i=1) and b, the Sequencer produces a signal on output terminal c_i.

When a Sequencer receives signals on b and both a_0 and a_1, it produces a signal on exactly one of the c_i-outputs (the other is delayed till the next b input arrives). The specification leaves the choice open. Often there is a fairness requirement on this choice: if a choice situation arises `infinitely often' then both outputs are chosen `infinitely often'.

Each pair of terminals (a_i, c_i) can be viewed as one passive 2-phase handshake port. A Sequencer `sequences' handshakes on its handshake ports in synchrony with signals on the b input. The b input is also referred to as next input.

XDI

Schematic diagram for a Sequencer:

[Zoom|FIG]

XDI state graph for a Sequencer:

[Zoom|FIG]

Specification in XDI model.

An enabled Sequencer has state 4 as initial state. In the connection diagram this is indicated with a dot on the inside at input b.

Verdect

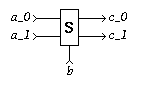
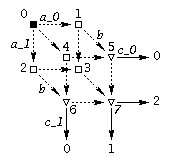
Specification in Verdect:


define SEQ( a0?, a1?, b?, c0!, c1! ) =
       pref *[ a0?; c0! ]
   ||  pref *[ a1?; c1! ]
   ||  pref *[ b?; (c0! | c1!) ]
end

Also available through this link

DI Algebra

Specification in DI Algebra:


I = { a0, a1, b }
O = { c0, c1 }

S = b?; [ a0? -> c0!; S , a1? -> c1!; S ]
.

Also available through this link

Properties

XDI Report.

The subscripts 0 and 1 can be interchanged systematically:
SEQ(a_0, a_1, b; c_0, c_1) = SEQ(a_1, a_0, b; c_1, c_0)

A Sequencer is not output deterministic, since there is an output choice in state 7. The output nondeterminism is dynamic.

Implementations

DI Decompositions

A Sequencer can be implemented with a Mixer and a Join (equ):

[Zoom|FIG]

Using Boolean Gates

No information available

Using Transistors