k-Sequencer

Specifications

Informal

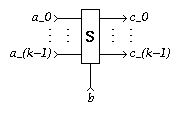
A k-Sequencer (k>0) has k+1 input terminals a_i (0<=i<k) and b, and k output terminals c_i (0<=i<k). It waits for a signal on at least one of the a inputs and a signal on the b input. In contrast to a k-Latch, the environment need not guarantee mutual exclusion of the a-inputs. Having received input signals on a_i (0<=i<k) and b, it produces a signal on output terminal c_i.

When a k-Sequencer receives signals on b and more than one a_i, it produces a signal on exactly one of the c_i-outputs (the others are delayed till the next b input arrives). The specification leaves the choice open. Often there is a fairness requirement on this choice: if a choice situation arises `infinitely often' then both outputs are chosen `infinitely often'.

Each pair of terminals (a_i, c_i) can be viewed as one passive 2-phase handshake port. A k-Sequencer `sequences' handshakes on its handshake ports in syncrhony with signals on the b input. The b input is also referred to as next input.

XDI

Schematic diagram for a k-Sequencer:

[Zoom|FIG]

XDI state graph and specification for a k-Sequencer with k=3:

[Zoom|FIG]

Specification in XDI model.

. (Not available for general k)

Verdect

Parameterized definitions are not possible in VERDECT, but this sketch gives the general idea:

Specification in Verdect:

define S( a0?, .., a(k-1)?, b?, c0!,.., c(k-1)! ) =
       pref *[ a0?; c0! ]
   ||  ...
   ||  pref *[ a(k-1)?; c(k-1)! ]
   ||  pref *[ b?; (c0! | ... | c(k-1)! ) ]
end

Also available through this link

DI Algebra

Pure DI Algebra does not allow a generalized specification. The following specification therefore needs instantiation before interpretation:

Specification in DI Algebra:

I = { a0, .. ,a(k-1)?, b? }
O = { c0!, .. , c(k-1)! }
S_k = b?; [ a0? -> c0!; S_k, ... , a(k-1)? -> c(k-1)!; S_k ]

Also available through this link

.
The specification of the case k=3 is as follows:

Specification in DI Algebra:

# Generated by expexp.pl
NAME ="S"
I    = { a0?, b?, a1?, a2? }
O    = { c0!, c1!, c2! }

S_3 = b?;[
	a0? -> c0!;S_3
, 	a1? -> c1!;S_3
, 	a2? -> c2!;S_3
	]

Also available through this link

Properties

XDI Report for the case k=3. (Not available for general k)

The roles of subscripts i can be permuted (on a and c simultaneously).

The k-Sequencer satisfies Rules Y' and Z^in, but not Z^out (choice between c outputs).

Implementations

DI Decompositions

A k-Sequencer with k=1 is a Join.
A k-Sequencer with k=2 is a Sequencer.
A k-Sequencer with k=(m+n) can be implemented with a k-mixer with k=m and a k-Sequencer with k=(n+1) (equ):

[Zoom|FIG]

Taking n=0, we find an implementation of a k-Sequencer (k=m) with a k-mixer with k=m and a Join.
With a little hunting we can find that for m>1, a k-mixer with k=m can be implemented with m-1 enabled Sequencers m-1 Latches 2m-2 Merges and 4m-4 Forks. By suitably combining this implementation with schemes 2 and 4 above, one can obtain implementations of a k-Sequencer (k=m) for arbitrary m>1, in terms of m-1 Sequencers (of which m-2 are enabled), m-2 Latches 2m-4 Merges 4m-8 Forks.

Using Boolean Gates

No information available

Using Transistors

No information available

k-Sequencer

Specifications

Informal

XDI

Verdect

DI Algebra

Properties

Implementations

DI Decompositions

Using Boolean Gates

Using Transistors

Generalizations

Miscellaneous

References

Last modified at Fri Nov 20 10:11:40 1998