k-Toggle

Specification in XDI model.

Verdect

Specification in Verdect:

define TOGGLE( a?, b0!, ..,  b(k-1)! ) =
       pref *[ a?; b0!; .. ; a?; b(k-1)! ]
end

DI Algebra

Specification in DI Algebra:

T(k) = T(k,0)

where

T(k,i) = a?; bi!; T(k,(i+1) mod k)

Specification in DI Algebra:

# Generated by expexp.pl
NAME ="T"
I    = { a? }
O    = { b0!, b1!, b2! }

T_0_3 = a?; b0!; T_1_3

T_1_3 = a?; b1!; T_2_3

T_2_3 = a?; b2!; T_0_3

Properties

T_k(a; b₀, b₁..., b_k-1) / a b₀ = T_k(a; b₁, ..., b_k-1, b₀)

The k-Toggle satisfies Rules Y' and Z'.

Implementations

1. A k-Toggle with k=1 is a Wire.
2. A k-Toggle with k=2 is a Toggle.
3. A k-Toggle can be implemented as a small state machine using a Latch by feeding output i to input (i+1) mod k (cf. Toggle Implementations).
4. For m>0 and n>0, a k-Toggle with k=mn can be implemented with one k-Toggle with k=m and m k-Toggles with k=n
   
   
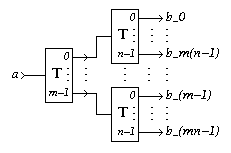
   [Zoom|FIG]
   
5. For k>0, a k-Toggle with k=m can be implemented by feeding back one output, say b_k, of a k-Toggle with k=m+1 with a Merge:
   
   
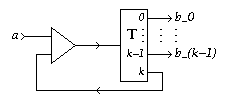
   [Zoom|FIG]
   
6. By suitably combining implementation schemes 2, 4 and 5 one can obtain implementations of k-Toggles for arbitrary k>0, in terms of Toggles and Merges. When k is a power of 2, only scheme 4 is needed (the result does not depend on whether k-Toggles with k=2 are introduced `on the left' or `on the right': the scheme is commutative for powers of 2 constructed in this way). The implementation of a k-Toggle with k=2^m requires 2^m-1 Toggles (no Merges).

   When k is not a power of 2 (hence, k>2), also scheme 5 is needed. In this case, the resulting implementation does depend on the order. For instance, consider the implementation of a k-Toggle with k=5. One can start with a k-Toggle with k=8. to reduce it to a k-Toggle with k=5. This results in an implementation with 7 Toggles and 3 Merges.

   Alternatively, we can first implement a k-Toggle with k=3 by reducing a k-Toggle with k=4 once according to scheme 5. This costs three Toggles and one Merge. Using scheme 4, the k-Toggle with k=3 can be made into a k-Toggle with k=6 by adding three Toggles `on the right'. The k-Toggle with k=6 can then be reduced to a k-Toggle with k=5 This implementation consists of 6 Toggles and 2 Merges.

   Using scheme 4 to make a k-Toggle with k=6 from one Toggle (`on the left') and two k-Toggles with k=3 results in yet another implementation, costing 7 Toggles and 3 Merges.

   Theorem: When constructing a k-Toggle with t Toggles and m Merges we must have k=t-m+1 and, hence, t>=k-1.

7. For m>0, n>0, and m and n relatively prime, a k-Toggle with k=mn can be implemented with one k-Toggle with k=m, one k-Toggle with k=n, and a Decision-Wait:
   
   
   [Zoom|FIG]
   

Using Boolean Gates

No information available

Using Transistors

No information available

Generalizations

Miscellaneous

Exercise: What is an optimal implementation scheme for k-Toggles in terms of Toggles and Merges. The cost function can either be size or `average response time'.

References

Last modified at Fri Nov 20 10:11:40 1998