k-Call

Specifications

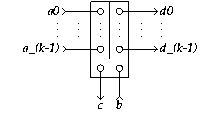
Informal

A k-Call (k>0) has k+1 input terminals a_i (0<=i<k) and b, and k+1 output terminals c and d_i (0<=i<k). A signal appearing on either of the a_i terminals will cause a signal to be produced at terminal c. The combination of a signal at terminal a_i and terminal b will cause a signal to be produced at terminal d_i. The environment must guarantee mutual exclusion of the a_i-inputs.

XDI

Schematic diagram for a k-Call:

[Zoom|FIG]

We provide XDI specifications for the 3-call:

Specification in XDI model.

the 4-call:

Specification in XDI model.

and the 5-call:

Specification in XDI model.

(Not available for general k.)

Verdect

Parameterized definitions are not possible in VERDECT, but this sketch gives the general idea:

Specification in Verdect:


define CALL[k]( a0?, ..., a(k-1)?, b?, c!, d0!, ..., d(k-1)! ) =
       pref *[ (a0? | ... | a(k-1)?); c! ]
    || pref *[ (a0? || b?); d0!
             | ...
             | (a(k-1)? || b?); d(k-1)!
             ]
end

Also available through this link

DI Algebra

Pure DI Algebra does not allow a generalized specification. The following specification therefore needs instantiation before interpretation:

Specification in DI Algebra:

CALL(k) = [(,i:0<= i < k: a_k? -> c!; C(i,k))]
C(i,k)  = [ b? -> d_i!; CALL(k), (,j: 0<= j < k: a_j? -> a_j? -> CHAOS)]

Also available through this link

We provide DI Algebra specifications for

the 3-call:
Specification in DI Algebra.
the 4-call:
Specification in DI Algebra.
and the 5-call:
Specification in DI Algebra.

Properties

As an example we give the XDI Report for the case k=3.

The roles of subscripts i can be permuted (on a_i and d_i simultaneously).

The k-Call satisfies Rules Y' and Z^out, but not Z^inp (choice between a_i inputs).

Implementations

DI Decompositions

A 2-Call is a Call.
A k-Call can be implemented with k Fork, a k-Merge and a k-Latch (equ):

[Zoom|FIG]
An (m+n)-Call can be implemented with an m-Call and an (n+1)-Call (equ):

[Zoom|FIG]

As an example we composed two 5-calls to form a 9-call. The Ludwig verification script of this implementation..

Using Boolean Gates

No information available

Using Transistors

No information available

k-Call

Specifications

Informal

XDI

Verdect

DI Algebra

Properties

Implementations

DI Decompositions

Using Boolean Gates

Using Transistors

Generalizations

Miscellaneous

References

Last modified at Fri Nov 20 10:11:40 1998