Modulo-N Counter

Specifications

Informal

A Modulo-N Counter (N > 0) has one input terminal a and two output terminals p and q. Input and output signals alternate, starting with input. The behavior repeats after every N input/output pairs. In each period, the first N-1 inputs are followed by output p, and the last input is followed by output q.

XDI

Schematic diagram for a Modulo-N Counter:

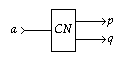
[Zoom|FIG]

Nor a state graph nor an XDI specification are available for general N. We provide them for N=3:

[Zoom|FIG]

Specification in XDI model.

Verdect

The specification of a Modulo-N Counter for N=3 is as follows:

Specification in Verdect:

define COUNTER3( a?, p!, q! ) =
       pref *[ a?; p!; a?; p!; a?; q! ]
end

Also available through this link

(Not available for general N.)

This verification report compares the Verdect specification with the XDI specification.

DI Algebra

We provide the specification for the case N=3:

Specification in DI Algebra:

# Generated by expexp.pl
NAME ="C"
I    = { a? }
O    = { p!, q! }

C_0_3 = a?;p!;C_1_3

C_1_3 = a?;p!;C_2_3

C_2_3 = a?;q!;C_0_3

Also available through this link

(Not available for general N.)

This verification report compares the DI Algebra specification with the XDI specification.

Properties

The XDI Report for the Modulo-3 Counter.

Implementations

DI Decompositions

[Ebergen92] analyses various implementations of Modulo-N Counters. A naive implementation (area complexity thetha(N), response time thetha(log N)) of A Modulo-N Counter for N>3 consists of an Nx1-Decision-Wait, an (N-1)-Merge, 3 Forks and an I-Wire:

The Ludwig verification script of this implementation. (N=3)
The verification report of this implementation (N=3).

Using Boolean Gates

No information available

Using Transistors

No information available

Generalizations

The Modulo-N Counter can be further generalized to a L-Pattern Generator that cycles through an arbitrary pattern over its outputs. A Modulo-N Counter is a (p..pq)-Pattern Generator (with N-1 p's).

Miscellaneous

No information available

References

[Ebergen92]

Modulo-N Counter

Informal

DI Decompositions

Using Boolean Gates

Using Transistors

Last modified at Fri Nov 20 13:30:44 1998